Matematika SMP Kelas VII: Bilangan Pecahan
Pengantar Pecahan
Bilangan Pecahan telah diajarkan sejak tingkat sekolah dasar. Hampir semua materi pecahan di SMP telah diajarkan di SD namun, yang membedakannya adalah peningkatan kesulitn materi akibat perbedaan pola pikir anak-anak terkait dengan pembelajaran matematika sekolah. Tentu saja di smp kelas VII, materi pecahan diajarkan dengan mulai sedikit demi sedikit meninggalkan model konkrit.
Pembelajaran matematika SMP Kelas VII semester 1 materi pecahan ditekankan untuk membantu siswa mencapai standar kompetensi yaitu memahami sifat-sifat operasi hitung bilangan dan penggunaanya dalam pemecahan masalah. Kompetensi dasarnya adalah melakukan operasi hitung bilangan pecahan; dan siswa diharapkan dapat menggunakan sifat-sifat hitung bilangan pecahandalam pemecahan masalah.
Materi pecahan yang diajarkan di SMP kelas VII antara lain: Pengertian Bilangan Pecahan, Pengertian dan Cara Menentukan Pecahan Senilai, Menyederhanakan Bilangan Pecahan, Menyatakan Hubungan Antara Dua Pecahan, Menentukan Letak Pecahan Pada Garis Bilangan, Menentukan Pecahan yang Nilainya di Antara Dua Pecahan, Pecahan sebagai Perbandingan Bagian dari Keseluruhan, Mengubah Pecahan Biasa Menjadi Pecahan Campuran, Mengubah Bentuk Pecahan ke Bentuk Desimal, Mengubah Bentuk Pecahan ke Bentuk Persen, Mengubah Bentuk Pecahan ke Bentuk Permil, Penjumlahan dan Pengurangan Pecahan, Sifat-sifat pada penjumlahan dan pengurangan pecahan, Operasi Perkalian Pecahan, Sifat-sifat dan Invers perkalian pada pecahan dan Operasi Pembagian Pecahan.
Pecahan (dalam bahasa inggris fraction, berasal dari kata Latin fractio yang berarti memecah. Oleh karena itu, istilah bilangan pecah juga sering juga disebut pecahan. Istilah pecahan dapat digunakan untuk merujuk suatu bilangan yang ditulis dalam bentuk 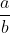 dimana b ≠ 0. Perlu diperhatikan penggunaan simbol tersebut sebagai bilangan atau angka.
dimana b ≠ 0. Perlu diperhatikan penggunaan simbol tersebut sebagai bilangan atau angka.
Misalnya, jika kita menyatakan bahwa bilangan yang terletak di atas disebut pembilang dan bilangan yang di bawah disebut penyebut, maka pecahan yang kita maksud di situ adalah suatu simbol atau angka. Akan tetapi jika kita mengatakan, “Jumlahkan 13 dan 12 ,” maka yang kita maksud adalah pecahan sebagai suatu bilangan.
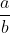 , bilangan b menunjukkan banyaknya bagian yang sama dalam keseluruhan, sedangkan bilangan yang di atas, a, menunjukkan banyaknya bagian yang diperhatikan. Gambar berikut ini menggambarkan pecahan 3⁄8.
, bilangan b menunjukkan banyaknya bagian yang sama dalam keseluruhan, sedangkan bilangan yang di atas, a, menunjukkan banyaknya bagian yang diperhatikan. Gambar berikut ini menggambarkan pecahan 3⁄8.
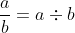
(3) Pecahan sebagai konsep perbandingan.
Pengertian dan Konsepsi dari Pecahan
Pecahan (dalam bahasa inggris fraction, berasal dari kata Latin fractio yang berarti memecah. Oleh karena itu, istilah bilangan pecah juga sering juga disebut pecahan. Istilah pecahan dapat digunakan untuk merujuk suatu bilangan yang ditulis dalam bentuk
Misalnya, jika kita menyatakan bahwa bilangan yang terletak di atas disebut pembilang dan bilangan yang di bawah disebut penyebut, maka pecahan yang kita maksud di situ adalah suatu simbol atau angka. Akan tetapi jika kita mengatakan, “Jumlahkan 13 dan 12 ,” maka yang kita maksud adalah pecahan sebagai suatu bilangan.
Pada topik pecahan di SMP, pembilang dan penyebut suatu pecahan adalah bilangan bulat. Bilangan yang seperti ini juga disebut dengan bilangan rasional. Akan tetapi, secara umum, pembilang dan pecahan suatu pecahan adalah sembarang bilangan real asalkan penyebutnya tidak sama dengan nol.
Pecahan dapat dijelaskan dengan menggunakan tiga konsep, yaitu konsep
Pecahan dapat dijelaskan dengan menggunakan tiga konsep, yaitu konsep
(1) Pecahan sebagai sebagian dari keseluruhan.
Pecahan dinyatakan sebagai konsep sebagian dari keseluruhan artinya pecahan digunakan untuk menytakan hubungan antara bagian-bagian dari sesuatu yang utuh. Pada pecahan
(2) Pecahan sebagai konsep pembagian
Konsep ini menyatakan pecahan sebagai hasil bagi suatu bilangan dengan bilangan yang lain. Konsep semacam ini dapat diilustrasikan dengan di bawah ini.
Untuk menentukan 3 ÷ 4, maka kita bagi 3 dengan 2 terlebih dahulu. Dari sini kita akan mendapatkan satu setengah. Setelah itu, kita bagi dua satu setengah tersebut untuk mendapatkan ¾.Konsep ini menyatakan pecahan sebagai hasil bagi suatu bilangan dengan bilangan yang lain. Konsep semacam ini dapat diilustrasikan dengan di bawah ini.

| Untuk sembarang bilangan a dan b, dengan b ≠ 0 |
Pecahan juga dapat digunakan sebagai perbandingan. Misalkan banyaknya siswa laki-laki adalah sepertiga dari banyaknya siswa perempuan.
Pecahan-Pecahan Senilai
Pecahan Senilai dan Cara Menentukan Pecahan Senilai- Pecahan yang berbeda dapat bernilai sama asalkan perbandingannya tetap. Pecahan tersebut dinamakan pecahan senilai. Pecahan senilai merupakan materi yang diajarkan pada siswa kelas 4 sekolah dasar dimana pada Kompetensi Dasar 3.1 Menentukan Pecahan Senilai dengan Membagi atau Mengalikan Pembilang dan Penyebut dengan Bilangan yang Sama. Kompetensi ini sangat penting dimiliki siswa kelas 4 karena akan sangat berguna sebagai materi prasyarat pada materi pecahan selanjutnya maupun materi materi matematika yang lain.



0 Comments